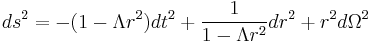Inflation (cosmology)

"Inflation model" and "Inflation theory" redirect here. For a general rise in the price level, see Inflation. For other uses, see Inflation (disambiguation).
Physical cosmology
Universe · Big Bang
Age of the universe
Timeline of the Big Bang
Ultimate fate of the universe
Early universe
Inflation · Nucleosynthesis
GWB · Neutrino background
Cosmic microwave background

In physical cosmology, cosmic inflation, cosmological inflation or just inflation is the theorized extremely rapid exponential expansion of the early universe by a factor of at least 1078 in volume, driven by a negative-pressure vacuum energy density.[1] The inflationary epoch comprises the first part of the electroweak epoch following the grand unification epoch. It lasted from 10−36 seconds after the Big Bang to sometime between 10−33 and 10−32 seconds. Following the inflationary period, the universe continued to expand, but at a slower rate.

The term "inflation" is also used to refer to the hypothesis that inflation occurred, to the theory of inflation, or to the inflationary epoch. The inflationary hypothesis was originally proposed in 1980 by American physicist Alan Guth, who named it "inflation".[2] It was also proposed by Katsuhiko Sato in 1981.[3]

As a direct consequence of this expansion, all of the observable universe originated in a small causally connected region. Inflation answers the classic conundrum of the Big Bang cosmology: why does the universe appear flat, homogeneous and isotropic in accordance with the cosmological principle when one would expect, on the basis of the physics of the Big Bang, a highly curved, heterogeneous universe? Inflation also explains the origin of the large-scale structure of the cosmos. Quantum fluctuations in the microscopic inflationary region, magnified to cosmic size, become the seeds for the growth of structure in the universe (see galaxy formation and evolution and structure formation).[4]

While the detailed particle physics mechanism responsible for inflation is not known, the basic picture makes a number of predictions that have been confirmed by observation. Inflation is thus now considered part of the standard hot Big Bang cosmology. The hypothetical particle or field thought to be responsible for inflation is called the inflaton.

Contents

Overview

Main article: Metric expansion of space

While special relativity constrains objects in the universe from moving faster than the speed of light with respect to each other, there is no such constraint in general relativity. An expanding universe generally has a cosmological horizon, and like a black hole event horizon, this marks the boundary to the part of the universe that an observer can see. The horizon is the boundary beyond which objects are moving away too fast to be visible from Earth.

There are two ways to describe a spacetime with a horizon: global and local. The global picture includes regions beyond the horizon, which are invisible to us, while the local picture is the picture from one point of view only. These two perspectives are related by a process of extension: wherever there is a horizon, a solution of General Relativity can go on by assuming that nothing special happens there. The local and global points of view have a different notion of time. From the local point of view, time stops at the horizon. From the global point of view, time marches on, and surfaces of constant time cross the horizon. Ignoring quantum mechanics, the two pictures are equivalent: any statement can be translated freely back and forth.

For cosmology in the global point of view, the observable universe is one causal patch of a much larger unobservable universe; there are parts of the universe which cannot communicate with us yet. These parts of the universe are outside our current cosmological horizon. In the standard hot big bang model, without inflation, the cosmological horizon moves out, bringing new regions into view. As we see these regions for the first time, they look no different from any other region of space we have already seen: they have a background radiation which is at nearly exactly the same temperature as the background radiation of other regions, and their space-time curvature is evolving lock-step with ours. This presents a mystery: how did these new regions know what temperature and curvature they were supposed to have? They couldn't have learned it by getting signals, because they were not in communication with our past light cone before.[5][6]

Inflation answers this question by postulating that all the regions come from an earlier era with a big vacuum energy, or cosmological constant. A space with a cosmological constant is qualitatively different: instead of moving outward, the cosmological horizon stays put. For any one observer, the distance to the cosmological horizon is constant. With exponentially expanding space, two nearby observers are separated very quickly; so much so, that the distance between them quickly exceeds the limits of communications. In the global point of view, the spatial slices are expanding very fast to cover huge volumes. In the local point of view, things are constantly moving beyond the cosmological horizon, which is a fixed distance away, and everything becomes homogeneous very quickly.

In either view, as the scalar field slowly relaxes to the vacuum, the cosmological constant goes to zero, and space begins to expand normally. The new regions which come into view during the normal expansion phase, in the global point of view, are exactly the same regions which were pushed out of the horizon during inflation, and so they are necessarily at nearly the same temperature and curvature, because they come from the same little patch of space. In the local point of view, the cosmological horizon still is at the big bang, and inflation is always going on in a thin skin where time is nearly stopped, and the same process produces new regions as it always did, up to small fluctuations.

Inflation from the global point of view is often called eternal inflation. On a global constant-time slice, regions with inflation have an exponentially growing volume, while regions which are not inflating don't. This means that the volume of the inflating part of the universe in the global picture is always unimaginably larger than the part that has stopped inflating. If the probability of different regions is counted by volume, one should expect that inflation will never end, or applying boundary conditions that we exist to observe it, that inflation will end as late as possible. Weighting by volume is unnatural in the local point of view where inflation is not eternal—it eventually ends as seen by any single observer. This picture gives a meaning to the probability distribution on the anthropic landscape, and naively seems more compatible with the holographic principle.

The theory of inflation in any picture explains why the temperatures and curvatures of different regions are so nearly equal, and it predicts that the total curvature of a space-slice at constant global time is zero. This prediction means that the total ordinary matter, dark matter, and residual vacuum energy in the universe have to add up to the critical density, a prediction which is very accurately confirmed. More strikingly, inflation allows physicists to calculate the minute differences in temperature of different regions from quantum fluctuations during the inflationary era, and these quantitative predictions have also been confirmed.

Space expands

To say that space expands exponentially means that two inertial observers are moving farther apart with accelerating velocity. In stationary coordinates for one observer, a patch of an inflating universe has the following polar metric:[7][8]

ds^2 = - (1- \Lambda r^2) dt^2 %2B {1\over 1-\Lambda r^2} dr^2 %2B r^2 d\Omega^2

This is just like an inside-out black hole metric—it has a zero in the 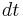dt component on a fixed radius sphere called the cosmological horizon. Objects are drawn away from the observer at 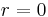r=0 towards the cosmological horizon, which they cross in a finite proper time. This means that any inhomogeneities are smoothed out, just as any bumps or matter on the surface of a black hole horizon are swallowed and disappear.

Since the space–time metric has no explicit time dependence, once an observer has crossed the cosmological horizon, observers closer in take its place. This process of falling outward and replacement points closer in are always steadily replacing points further out—an exponential expansion of space–time.

This steady-state exponentially expanding spacetime is called a de Sitter space, and to sustain it there must be a cosmological constant, a vacuum energy proportional to 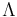\Lambda everywhere. In this case, the equation of state is 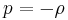\! p=-\rho. The physical conditions from one moment to the next are stable: the rate of expansion, called the Hubble parameter, is nearly constant, and the scale factor of the universe is proportional to 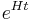e^{Ht}. Inflation is often called a period of accelerated expansion because the distance between two fixed observers is increasing exponentially (i.e. at an accelerating rate as they move apart), while \Lambda can stay approximately constant (see deceleration parameter).

Few inhomogeneities remain

Cosmological inflation has the important effect of smoothing out inhomogeneities, anisotropies and the curvature of space. This pushes the universe into a very simple state, in which it is completely dominated by the inflaton field, the source of the cosmological constant, and the only significant inhomogeneities are the tiny quantum fluctuations in the inflaton. Inflation also dilutes exotic heavy particles, such as the magnetic monopoles predicted by many extensions to the Standard Model of particle physics. If the universe was only hot enough to form such particles before a period of inflation, they would not be observed in nature, as they would be so rare that it is quite likely that there are none in the observable universe. Together, these effects are called the inflationary "no-hair theorem"[9] by analogy with the no hair theorem for black holes.

The "no-hair" theorem works essentially because the cosmological horizon is no different from a black-hole horizon, except for philosophical disagreements about what is on the other side. The interpretation of the no-hair theorem is that the universe (observable and unobservable) expands by an enormous factor during inflation. In an expanding universe, energy densities generally fall, or get diluted, as the volume of the universe increases. For example, the density of ordinary "cold" matter (dust) goes as the inverse of the volume: when linear dimensions double, the energy density goes down by a factor of eight; the radiation energy density goes down even more rapidly as the universe expands since the wavelength of each photon is stretched (redshifted), in addition to the photons being dispersed by the expansion. When linear dimensions are doubled, the energy density in radiation falls by a factor of sixteen. During inflation, the energy density in the inflaton field is roughly constant. However, the energy density in inhomogeneities, curvature, anisotropies and exotic particles is falling, and through sufficient inflation these become negligible. This leaves an empty, flat, and symmetric universe, which is filled with radiation when inflation ends.

Key requirement

A key requirement is that inflation must continue long enough to produce the present observable universe from a single, small inflationary Hubble volume. This is necessary to ensure that the universe appears flat, homogeneous and isotropic at the largest observable scales. This requirement is generally thought to be satisfied if the universe expanded by a factor of at least 1026 during inflation.[10]

Reheating

Inflation is a period of supercooled expansion, when the temperature drops by a factor of 100,000 or so. (The exact drop is model dependent, but in the first models it was typically from 1027K down to 1022K.[11]) This relatively low temperature is maintained during the inflationary phase. When inflation ends the temperature returns to the pre-inflationary temperature; this is called reheating or thermalization because the large potential energy of the inflaton field decays into particles and fills the universe with Standard Model particles, including electromagnetic radiation, starting the radiation dominated phase of the Universe. Because the nature of the inflation is not known, this process is still poorly understood, although it is believed to take place through a parametric resonance.[12][13]

Motivation

Inflation resolves several problems in the Big Bang cosmology that were pointed out in the 1970s.[14] Inflation was first discovered by Guth while investigating the problem of why we see no magnetic monopoles today; he found that a positive-energy false vacuum would, according to general relativity, generate an exponential expansion of space. It was very quickly realised that such an expansion would resolve many other long-standing problems. These problems arise from the observation that to look like it does today, the universe would have to have started from very finely tuned, or "special" initial conditions at the Big Bang. Inflation attempts to resolve these problems by providing a dynamical mechanism that drives the universe to this special state, thus making a universe like ours much more likely in the context of the Big Bang theory.

Magnetic-monopole problem

The magnetic-monopole problem (sometimes called the exotic-relics problem) says that if the early universe were very hot, a large number of very heavy, stable magnetic monopoles would be produced. This is a problem with Grand Unified Theories, which proposes that at high temperatures (such as in the early universe) the electromagnetic force, strong and weak nuclear forces are not actually fundamental forces but arise due to spontaneous symmetry breaking from a single gauge theory.[15] These theories predict a number of heavy, stable particles that have not yet been observed in nature. The most notorious is the magnetic monopole, a kind of stable, heavy "knot" in the magnetic field.[16][17] Monopoles are expected to be copiously produced in Grand Unified Theories at high temperature,[18][19] and they should have persisted to the present day, to such an extent that they would become the primary constituent of the universe.[20][21] Not only is that not the case, but all searches for them have so far turned out fruitless, placing stringent limits on the density of relic magnetic monopoles in the universe.[22] A period of inflation that occurs below the temperature where magnetic monopoles can be produced would offer a possible resolution of this problem: monopoles would be separated from each other as the universe around them expands, potentially lowering their observed density by many orders of magnitude. Though, as Martin Rees has written, "Skeptics about exotic physics might not be hugely impressed by a theoretical argument to explain the absence of particles that are themselves only hypothetical. Preventive medicine can readily seem 100 percent effective against a disease that doesn't exist!"[23]

Horizon problem

Main article: Horizon problem

The horizon problem[24][25][26] is the problem of determining why the universe appears statistically homogeneous and isotropic in accordance with the cosmological principle. For example, molecules in a canister of gas are distributed homogeneously and isotropically because they are in thermal equilibrium: gas throughout the canister has had enough time to interact to dissipate inhomogeneities and anisotropies. The situation is quite different in the big bang model without inflation, because gravitational expansion does not give the early universe enough time to equilibrate. In a big bang with only the matter and radiation known in the Standard Model, two widely separated regions of the observable universe cannot have equilibrated because they move apart from each other faster than the speed of light—thus have never come in to causal contact: in the history of the universe, back to the earliest times, it has not been possible to send a light signal between the two regions. Because they have no interaction, it is difficult to explain why they have the same temperature (are thermally equilibrated). This is because the Hubble radius in a radiation or matter-dominated universe expands much more quickly than physical lengths and so points that are out of communication are coming into communication. Historically, two proposed solutions were the Phoenix universe of Georges Lemaître[27] and the related oscillatory universe of Richard Chase Tolman,[28] and the Mixmaster universe of Charles Misner.[25][29] Lemaître and Tolman proposed that a universe undergoing a number of cycles of contraction and expansion could come into thermal equilibrium. Their models failed, however, because of the buildup of entropy over several cycles. Misner made the (ultimately incorrect) conjecture that the Mixmaster mechanism, which made the universe more chaotic, could lead to statistical homogeneity and isotropy.

Flatness problem

Main article: Flatness problem

Another problem is the flatness problem (which is sometimes called one of the Dicke coincidences, with the other being the cosmological constant problem).[30][31] It had been known in the 1960s that the density of matter in the universe was comparable to the critical density necessary for a flat universe (that is, a universe whose large scale geometry is the usual Euclidean geometry, rather than a non-Euclidean hyperbolic or spherical geometry).

Therefore, regardless of the shape of the universe the contribution of spatial curvature to the expansion of the universe could not be much greater than the contribution of matter. But as the universe expands, the curvature redshifts away more slowly than matter and radiation. Extrapolated into the past, this presents a fine-tuning problem because the contribution of curvature to the universe must be exponentially small (sixteen orders of magnitude less than the density of radiation at big bang nucleosynthesis, for example). This problem is exacerbated by recent observations of the cosmic microwave background that have demonstrated that the universe is flat to the accuracy of a few percent.[32]

History

Precursors

In the early days of General Relativity, Albert Einstein introduced the cosmological constant to allow a static solution which was a three dimensional sphere with a uniform density of matter. A little later, Willem de Sitter found a highly symmetric inflating universe, which described a universe with a cosmological constant which is otherwise empty.[33] It was discovered that Einstein's solution is unstable, and if there are small fluctuations, it eventually turns into de Sitter's.

In the early 1970s Zeldovich noticed the serious flatness and horizon problems of big bang cosmology; before his work, cosmology was presumed to be symmetrical on purely philosophical grounds. In the Soviet Union, this and other considerations led Belinski and Khalatnikov to analyze the chaotic BKL singularity in General Relativity. Misner's Mixmaster universe attempted to use this chaotic behavior to solve the cosmological problems, with limited success.

In the late 1970s, Sidney Coleman applied the instanton techniques developed by Alexander Polyakov and collaborators to study the fate of the false vacuum in quantum field theory. Like a metastable phase in statistical mechanics—water below the freezing temperature or above the boiling point—a quantum field would need to nucleate a large enough bubble of the new vacuum, the new phase, in order to make a transition. Coleman found the most likely decay pathway for vacuum decay and calculated the inverse lifetime per unit volume. He eventually noted that gravitational effects would be significant, but he did not calculate these effects and did not apply the results to cosmology.

In the Soviet Union, Starobinsky noted that quantum corrections to general relativity should be important in the early universe, and these generically lead to curvature-squared corrections to the Einstein–Hilbert action. The solution to Einstein's equations in the presence of curvature squared terms, when the curvatures are large, can lead to an effective cosmological constant, so he proposed that the early universe went through a deSitter phase, an inflationary era.[34] This resolved the problems of cosmology, and led to specific predictions for the corrections to the microwave background radiation, corrections which were calculated in detail shortly afterwards.

In 1978, Zeldovich noted the monopole problem, which was an unambiguous quantitative version of the horizon problem, this time in a fashionable subfield of particle physics, which led to several speculative attempts to resolve it. In 1980, working in the west, Alan Guth realized that false vacuum decay in the early universe would solve the problem, leading him to propose scalar driven inflation. Starobinski's and Guth's scenarios both predicted an initial deSitter phase, differing only in the details of the mechanism.

Early inflationary models

Inflation was proposed in January, 1980 by Alan Guth as a mechanism for resolving these problems.[35][36] At the same time, Alexei Starobinsky argued that quantum corrections to gravity would replace the initial singularity of the universe with an exponentially expanding deSitter phase.[37] In October 1980 Demosthenes Kazanas suggested that exponential expansion could eliminate the particle horizon and perhaps solve the horizon problem,[38] and Sato suggesting that an exponential expansion could eliminate domain walls (another kind of exotic relic.)[39] In 1981 Einhorn and Sato[40] published a model similar to Guth's and showed that it would resolve the puzzle of the magnetic monopole abundance in Grand Unified Theories. Like Guth, they concluded that such a model not only required fine tuning of the cosmological constant, but also would very likely lead to a much too granular universe, i.e., to large density variations resulting from bubble wall collisions.

Guth proposed that as the early universe cooled, it was trapped in a false vacuum with a high energy density, which is much like a cosmological constant. As the very early universe cooled it was trapped in a metastable state (it was supercooled) which it could only decay out of through the process of bubble nucleation via quantum tunneling. Bubbles of true vacuum spontaneously form in the sea of false vacuum and rapidly begin expanding at the speed of light. Guth recognized that this model was problematic because the model did not reheat properly: when the bubbles nucleated, they did not generate any radiation. Radiation could only be generated in collisions between bubble walls. But if inflation lasted long enough to solve the initial conditions problems, collisions between bubbles became exceedingly rare. In any one causal patch it is likely that only one bubble will nucleate.

Slow-roll inflation

The bubble collision problem was solved by Andrei Linde[41] and independently by Andreas Albrecht and Paul Steinhardt[42] in a model named new inflation or slow-roll inflation (Guth's model then became known as old inflation). In this model, instead of tunneling out of a false vacuum state, inflation occurred by a scalar field rolling down a potential energy hill. When the field rolls very slowly compared to the expansion of the universe, inflation occurs. However, when the hill becomes steeper, inflation ends and reheating can occur.

Effects of asymmetries

Eventually, it was shown that new inflation does not produce a perfectly symmetric universe, but that tiny quantum fluctuations in the inflaton are created. These tiny fluctuations form the primordial seeds for all structure created in the later universe. These fluctuations were first calculated by Viatcheslav Mukhanov and G. V. Chibisov in the Soviet Union in analyzing Starobinsky's similar model.[43][44][45] In the context of inflation, they were worked out independently of the work of Mukhanov and Chibisov at the three-week 1982 Nuffield Workshop on the Very Early Universe at Cambridge University.[46] The fluctuations were calculated by four groups working separately over the course of the workshop: Stephen Hawking;[47] Starobinsky;[48] Guth and So-Young Pi;[49] and James M. Bardeen, Paul Steinhardt and Michael Turner.[50]

Observational status

Inflation is a concrete mechanism for realizing the cosmological principle which is the basis of the standard model of physical cosmology: it accounts for the homogeneity and isotropy of the observable universe. In addition, it accounts for the observed flatness and absence of magnetic monopoles. Since Guth's early work, each of these observations has received further confirmation, most impressively by the detailed observations of the cosmic microwave background made by the Wilkinson Microwave Anisotropy Probe (WMAP) spacecraft.[51] This analysis shows that the universe is flat to an accuracy of at least a few percent, and that it is homogeneous and isotropic to a part in 10,000.

In addition, inflation predicts that the structures visible in the universe today formed through the gravitational collapse of perturbations which were formed as quantum mechanical fluctuations in the inflationary epoch. The detailed form of the spectrum of perturbations called a nearly-scale-invariant Gaussian random field (or Harrison-Zel'dovich spectrum) is very specific and has only two free parameters, the amplitude of the spectrum and the spectral index which measures the slight deviation from scale invariance predicted by inflation (perfect scale invariance corresponds to the idealized de Sitter universe).[52] Inflation predicts that the observed perturbations should be in thermal equilibrium with each other (these are called adiabatic or isentropic perturbations). This structure for the perturbations has been confirmed by the WMAP spacecraft and other cosmic microwave background experiments,[51] and galaxy surveys, especially the ongoing Sloan Digital Sky Survey.[53] These experiments have shown that the one part in 10,000 inhomogeneities observed have exactly the form predicted by theory. Moreover, there is evidence for a slight deviation from scale invariance. The spectral index, ns is equal to one for a scale-invariant spectrum. The simplest models of inflation predict that this quantity is between 0.92 and 0.98.[54][55][56][57] From the data taken by the WMAP spacecraft it can be inferred that ns = 0.963 ± 0.012,[58] implying that it differs from one at the level of two standard deviations (2σ). This is considered an important confirmation of the theory of inflation.[51]

A number of theories of inflation have been proposed that make radically different predictions, but they generally have much more fine tuning than is necessary.[54][55] As a physical model, however, inflation is most valuable in that it robustly predicts the initial conditions of the universe based on only two adjustable parameters: the spectral index (that can only change in a small range) and the amplitude of the perturbations. Except in contrived models, this is true regardless of how inflation is realized in particle physics.

Occasionally, effects are observed that appear to contradict the simplest models of inflation. The first-year WMAP data suggested that the spectrum might not be nearly scale-invariant, but might instead have a slight curvature.[59] However, the third-year data revealed that the effect was a statistical anomaly.[51] Another effect has been remarked upon since the first cosmic microwave background satellite, the Cosmic Background Explorer: the amplitude of the quadrupole moment of the cosmic microwave background is unexpectedly low and the other low multipoles appear to be preferentially aligned with the ecliptic plane. Some have claimed that this is a signature of non-Gaussianity and thus contradicts the simplest models of inflation. Others have suggested that the effect may be due to other new physics, foreground contamination, or even publication bias.[60]

An experimental program is underway to further test inflation with more precise measurements of the cosmic microwave background. In particular, high precision measurements of the so-called "B-modes" of the polarization of the background radiation will be evidence of the gravitational radiation produced by inflation, and they will also show whether the energy scale of inflation predicted by the simplest models (1015–1016 GeV) is correct.[55][56] These measurements are expected to be performed by the Planck spacecraft, although it is unclear if the signal will be visible, or if contamination from foreground sources will interfere with these measurements.[61] Other forthcoming measurements, such as those of 21 centimeter radiation (radiation emitted and absorbed from neutral hydrogen before the first stars turned on), may measure the power spectrum with even greater resolution than the cosmic microwave background and galaxy surveys, although it is not known if these measurements will be possible or if interference with radio sources on earth and in the galaxy will be too great.[62]

Dark energy is broadly similar to inflation, and is thought to be causing the expansion of the present-day universe to accelerate. However, the energy scale of dark energy is much lower, 10−12 GeV, roughly 27 orders of magnitude less than the scale of inflation.

Theoretical status

Unsolved problems in physics
Is the theory of cosmological inflation correct, and if so, what are the details of this epoch? What is the hypothetical inflaton field giving rise to inflation?

In the early proposal of Guth, it was thought that the inflaton was the Higgs field, the field which explains the mass of the elementary particles.[36] It is now known that the inflaton cannot be the Higgs field.[63] Other models of inflation relied on the properties of grand unified theories.[42] Since the simplest models of grand unification have failed, it is now thought by many physicists that inflation will be included in a supersymmetric theory like string theory or a supersymmetric grand unified theory. A promising suggestion is brane inflation. At present, however, while inflation is understood principally by its detailed predictions of the initial conditions for the hot early universe, the particle physics is largely ad hoc modelling. As such, though predictions of inflation have been consistent with the results of observational tests, there are many open questions about the theory.

Fine-tuning problem

One of the most severe challenges for inflation arises from the need for fine tuning in inflationary theories. In new inflation, the slow-roll conditions must be satisfied for inflation to occur. The slow-roll conditions say that the inflaton potential must be flat (compared to the large vacuum energy) and that the inflaton particles must have a small mass.[64] In order for the new inflation theory of Linde, Albrecht and Steinhardt to be successful, therefore, it seemed that the universe must have a scalar field with an especially flat potential and special initial conditions.

Andrei Linde

Andrei Linde proposed a theory known as chaotic inflation in which he suggested that the conditions for inflation are actually satisfied quite generically and inflation will occur in virtually any universe that begins in a chaotic, high energy state and has a scalar field with unbounded potential energy.[65] However, in his model the inflaton field necessarily takes values larger than one Planck unit: for this reason, these are often called large field models and the competing new inflation models are called small field models. In this situation, the predictions of effective field theory are thought to be invalid, as renormalization should cause large corrections that could prevent inflation.[66] This problem has not yet been resolved and some cosmologists argue that the small field models, in which inflation can occur at a much lower energy scale, are better models of inflation.[67] While inflation depends on quantum field theory (and the semiclassical approximation to quantum gravity) in an important way, it has not been completely reconciled with these theories.

Robert Brandenberger has commented on fine-tuning in another situation.[68] The amplitude of the primordial inhomogeneities produced in inflation is directly tied to the energy scale of inflation. There are strong suggestions that this scale is around 1016 GeV or 10−3 times the Planck energy. The natural scale is naïvely the Planck scale so this small value could be seen as another form of fine-tuning (called a hierarchy problem): the energy density given by the scalar potential is down by 10−12 compared to the Planck density. This is not usually considered to be a critical problem, however, because the scale of inflation corresponds naturally to the scale of gauge unification.

Eternal inflation

Main article: Chaotic inflation

Cosmological inflation seems to be eternal the way it is theorised. Although new inflation is classically rolling down the potential, quantum fluctuations can sometimes bring it back up to previous levels. These regions in which the inflaton fluctuates upwards expand much faster than regions in which the inflaton has a lower potential energy, and tend to dominate in terms of physical volume. This steady state, which first developed by Vilenkin,[69] is called "eternal inflation". It has been shown that any inflationary theory with an unbounded potential is eternal.[70] It is a popular belief among physicists that this steady state cannot continue forever into the past.[71][72][73] The inflationary spacetime, which is similar to de Sitter space, is incomplete without a contracting region. However, unlike de Sitter space, fluctuations in a contracting inflationary space will collapse to form a gravitational singularity, a point where densities become infinite. Therefore, it is necessary to have a theory for the universe's initial conditions. Linde, however, believes inflation may be past eternal.[74]

Initial conditions

Some physicists have tried to avoid the initial conditions problem by proposing models for an eternally inflating universe with no origin.[75][76][77][78] These models propose that while the universe, on the largest scales, expands exponentially it was, is and always will be, spatially infinite and has existed, and will exist, forever.

Other proposals attempt to describe the ex nihilo creation of the universe based on quantum cosmology and the following inflation. Vilenkin put forth one such scenario.[69] Hartle and Hawking offered the no-boundary proposal for the initial creation of the universe in which inflation comes about naturally.[79]

Alan Guth has described the inflationary universe as the "ultimate free lunch":[80][81] new universes, similar to our own, are continually produced in a vast inflating background. Gravitational interactions, in this case, circumvent (but do not violate) the first law of thermodynamics (energy conservation) and the second law of thermodynamics (entropy and the arrow of time problem). However, while there is consensus that this solves the initial conditions problem, some have disputed this, as it is much more likely that the universe came about by a quantum fluctuation. Donald Page was an outspoken critic of inflation because of this anomaly.[82] He stressed that the thermodynamic arrow of time necessitates low entropy initial conditions, which would be highly unlikely. According to them, rather than solving this problem, the inflation theory further aggravates it – the reheating at the end of the inflation era increases entropy, making it necessary for the initial state of the Universe to be even more orderly than in other Big Bang theories with no inflation phase.

Hawking and Page later found ambiguous results when they attempted to compute the probability of inflation in the Hartle-Hawking initial state.[83] Other authors have argued that, since inflation is eternal, the probability doesn't matter as long as it is not precisely zero: once it starts, inflation perpetuates itself and quickly dominates the universe. However, Albrecht and Lorenzo Sorbo have argued that the probability of an inflationary cosmos, consistent with today's observations, emerging by a random fluctuation from some pre-existent state, compared with a non-inflationary cosmos overwhelmingly favours the inflationary scenario, simply because the "seed" amount of non-gravitational energy required for the inflationary cosmos is so much less than any required for a non-inflationary alternative, which outweighs any entropic considerations.[84]

Another problem that has occasionally been mentioned is the trans-Planckian problem or trans-Planckian effects.[85] Since the energy scale of inflation and the Planck scale are relatively close, some of the quantum fluctuations which have made up the structure in our universe were smaller than the Planck length before inflation. Therefore, there ought to be corrections from Planck-scale physics, in particular the unknown quantum theory of gravity. There has been some disagreement about the magnitude of this effect: about whether it is just on the threshold of detectability or completely undetectable.[86]

Hybrid inflation

Another kind of inflation, called hybrid inflation, is an extension of new inflation. It introduces additional scalar fields, so that while one of the scalar fields is responsible for normal slow roll inflation, another triggers the end of inflation: when inflation has continued for sufficiently long, it becomes favorable to the second field to decay into a much lower energy state.[87]

In hybrid inflation, one of the scalar fields is responsible for most of the energy density (thus determining the rate of expansion), while the other is responsible for the slow roll (thus determining the period of inflation and its termination). Thus fluctuations in the former inflaton would not affect inflation termination, while fluctuations in the latter would not affect the rate of expansion. Therefore hybrid inflation is not eternal.[88][89] When the second (slow-rolling) inflaton reaches the bottom of its potential, it changes the location of the minimum of the first inflaton's potential, which leads to a fast roll of the inflaton down its potential, leading to termination of inflation.

Inflation and string cosmology

The discovery of flux compactifications have opened the way for reconciling inflation and string theory.[90] A new theory, called brane inflation suggests that inflation arises from the motion of D-branes[91] in the compactified geometry, usually towards a stack of anti-D-branes. This theory, governed by the Dirac-Born-Infeld action, is very different from ordinary inflation. The dynamics are not completely understood. It appears that special conditions are necessary since inflation occurs in tunneling between two vacua in the string landscape. The process of tunneling between two vacua is a form of old inflation, but new inflation must then occur by some other mechanism.

Inflation and loop quantum gravity

When investigating the effects the theory of loop quantum gravity would have on cosmology, a loop quantum cosmology model has evolved that provides a possible mechanism for cosmological inflation. Loop quantum gravity assumes a quantized spacetime. If the energy density is larger than can be held by the quantized spacetime, it is thought to bounce back.

Criticisms

Since its introduction by Alan Guth in 1980, the inflationary paradigm has become widely accepted. Nevertheless, several physicists, mathematicians and philosophers of science have voiced criticisms, claiming unfulfilled promises and lack of serious empirical support. In 1999, John Earman and Jesús Mosterín published a thorough critical review of inflationary cosmology, concluding that “we do not think that there are, as yet, good grounds for admitting any of the models of inflation into the standard core of cosmology”.[92] Since 1999 the results of the WMAP mission in 2006 made the empirical case for cosmic inflation very compelling.

In order to work, and as pointed out by Roger Penrose from 1986 on, inflation requires extremely specific initial conditions of its own, so that the problem (or pseudoproblem) of initial conditions is not solved: “There is something fundamentally misconceived about trying to explain the uniformity of the early universe as resulting from a thermalization process. […] For, if the thermalization is actually doing anything […] then it represents a definite increasing of the entropy. Thus, the universe would have been even more special before the thermalization than after.”[93] The problem of specific or “fine-tuned” initial conditions would not have been solved; it would have gotten worse.

A recurrent criticism of inflation is that the invoked inflation field does not correspond to any known physical field, and that its potential energy curve seems to be an ad hoc contrivance to accommodate almost any data we could get. It is significant that Paul J. Steinhardt, one of the founding fathers of inflationary cosmology, has recently become one of its sharpest critics. He calls ‘bad inflation’ a period of accelerated expansion whose outcome conflicts with observations, and ‘good inflation’ one compatible with them: “Not only is bad inflation more likely than good inflation, but no inflation is more likely than either. … Roger Penrose considered all the possible configurations of the inflaton and gravitational fields. Some of these configurations lead to inflation … Other configurations lead to a uniform, flat universe directly –without inflation. Obtaining a flat universe is unlikely overall. Penrose’s shocking conclusion, though, was that obtaining a flat universe without inflation is much more likely than with inflation –by a factor of 10 to the googol (10 to the 100) power!”[94]

Adjuncts to inflation

There are models that explain some of the observations explained by inflation. However none of these "alternatives" has the same breadth of explanation as inflation, and still require inflation for a more complete fit with observation; they should therefore be regarded as adjuncts to inflation, rather than as alternatives.

String theory requires that, in addition to the three spatial dimensions we observe, there exist additional dimensions that are curled up or compactified (see also Kaluza-Klein theory). Extra dimensions appear as a frequent component of supergravity models and other approaches to quantum gravity. This raises the question of why four space-time dimensions became large and the rest became unobservably small. An attempt to address this question, called string gas cosmology, was proposed by Robert Brandenberger and Cumrun Vafa.[95] This model focuses on the dynamics of the early universe considered as a hot gas of strings. Brandenberger and Vafa show that a dimension of spacetime can only expand if the strings that wind around it can efficiently annihilate each other. Each string is a one-dimensional object, and the largest number of dimensions in which two strings will generically intersect (and, presumably, annihilate) is three. Therefore, one argues that the most likely number of non-compact (large) spatial dimensions is three. Current work on this model centers on whether it can succeed in stabilizing the size of the compactified dimensions and produce the correct spectrum of primordial density perturbations. For a recent review, see[96] The authors admits that their model "does not solve the entropy and flatness problems of standard cosmology ..... and we can provide no explanation for why the current universe is so close to being spatially flat."[97]

The ekpyrotic and cyclic models are also considered adjuncts to inflation. These models solve the horizon problem through an expanding epoch well before the Big Bang, and then generate the required spectrum of primordial density perturbations during a contracting phase leading to a Big Crunch. The universe passes through the Big Crunch and emerges in a hot Big Bang phase. In this sense they are reminiscent of the oscillatory universe proposed by Richard Chace Tolman: however in Tolman's model the total age of the universe is necessarily finite, while in these models this is not necessarily so. Whether the correct spectrum of density fluctuations can be produced, and whether the universe can successfully navigate the Big Bang/Big Crunch transition, remains a topic of controversy and current research. They also provide no explanation of the magnetic monopole problem. Unfortunately, as things stand - there is no evidence of any 'slowing down' of the expansion.

Another adjunct, the varying speed of light model has also been theorized by Jean-Pierre Petit in 1988, John Moffat in 1992 as well Andreas Albrecht and João Magueijo in 1999, instead of superluminal expansion the speed of light was 60 orders of magnitude faster than its current value solving the horizon and homogeneity problems in the early universe.

See also

Notes

  1. ^ Liddle and Lyth (2000) and Mukhanov (2005) are recent cosmology text books with extensive discussions of inflation. Kolb and Turner (1988) and Linde (1990) miss some recent developments, but are still widely used. Peebles (1993) provides a technical discussion with historical context. Recent review articles are Lyth and Riotto (1999) and Linde (2005). Guth (1997) and Hawking (1998) give popular introductions to inflation with historical remarks.
  2. ^ Chapter 17 of Peebles (1993).
  3. ^ Sato, K. (1981). "First-order phase transition of a vacuum and the expansion of the Universe". Monthly Notices of Royal Astronomical Society 195: 467. Bibcode 1981MNRAS.195..467S. 
  4. ^ Tyson, Neil deGrasse and Donald Goldsmith (2004), Origins: Fourteen Billion Years of Cosmic Evolution, W. W. Norton & Co., pp. 84-5.
  5. ^ Using Tiny Particles To Answer Giant Questions. Science Friday, 3 April 2009.
  6. ^ See also Faster than light#Universal_expansion.
  7. ^ Melia, Fulvio (2007), The Cosmic Horizon, MNRAS, 382, 1917--1921.
  8. ^ Melia, Fulvio et al. (2009), The Cosmological Spacetime, IJMP-D, 18, 1889--1901.
  9. ^ Kolb and Turner (1988).
  10. ^ This is usually quoted as 60 e-folds of expansion, where e60 ≈ 1026. It is equal to the amount of expansion since reheating, which is roughly Einflation/T0, where T0 = 2.7 K is the temperature of the cosmic microwave background today. See, e.g. Kolb and Turner (1998) or Liddle and Lyth (2000).
  11. ^ Guth, Phase transitions in the very early universe, in The Very Early Universe, ISBN 0521316774 eds Hawking, Gibbon & Siklos
  12. ^ See Kolb and Turner (1988) or Mukhanov (2005).
  13. ^ Kofman, Lev; Linde, Andrei; Starobinsky, Alexei (1994). "Reheating after inflation". Phys. Rev. Lett. 73 (5): 3195–3198. arXiv:hep-th/9405187. Bibcode 1986CQGra...3..811K. doi:10.1088/0264-9381/3/5/011. 
  14. ^ Much of the historical context is explained in chapters 15–17 of Peebles (1993).
  15. ^ Since supersymmetric Grand Unified Theory is built into string theory, it is still a triumph for inflation that it is able to deal with these magnetic relics. See, e.g. Kolb and Turner (1988) and Raby, Stuart (2006). "Grand Unified Theories". In ed. Bruce Hoeneisen. Galapagos World Summit on Physics Beyond the Standard Model. arXiv:hep-ph/0608183. 
  16. ^ 't Hooft, Gerard (1974). "Magnetic monopoles in Unified Gauge Theories". Nucl. Phys. B79: 276–84. 
  17. ^ Polyakov, Alexander M. (1974). "Particle spectrum in quantum field theory". JETP Lett. 20: 194–5. Bibcode 1974JETPL..20..194P. 
  18. ^ Guth, Alan; Tye, S. (1980). "Phase Transitions and Magnetic Monopole Production in the Very Early Universe". Phys.Rev.Lett. 44 (10): 631–635; Erratum ibid.,44:963, 1980. Bibcode 1980PhRvL..44..631G. doi:10.1103/PhysRevLett.44.631. 
  19. ^ Einhorn, Martin B (1980). "Are Grand Unified Theories Compatible with Standard Cosmology?". Phys. Rev. D21: 3295–3298. 
  20. ^ Zel'dovich, Ya.; M. Yu. Khlopov (1978). "On the concentration of relic monopoles in the universe". Phys. Lett. B79: 239–41. 
  21. ^ Preskill, John (1979). "Cosmological production of superheavy magnetic monopoles". Phys. Rev. Lett. 43 (19): 1365. Bibcode 1979PhRvL..43.1365P. doi:10.1103/PhysRevLett.43.1365. 
  22. ^ See, e.g. Yao, W.–M. (2006). "Review of Particle Physics". J. Phys. G 33 (1): 1. arXiv:astro-ph/0601168. Bibcode 2006JPhG...33....1Y. doi:10.1088/0954-3899/33/1/001. http://pdg.lbl.gov/. 
  23. ^ Rees, Martin. (1998). Before the Beginning (New York: Basic Books) p. 185
  24. ^ Misner, Charles W.; Coley, A A; Ellis, G F R; Hancock, M (1968). "The isotropy of the universe". Astrophysical Journal 151 (2): 431. Bibcode 1998CQGra..15..331W. doi:10.1088/0264-9381/15/2/008. 
  25. ^ a b Misner, Charles; Thorne, Kip S. and Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. pp. 489–490, 525–526. ISBN 0-7167-0344-0. 
  26. ^ Weinberg, Steven (1971). Gravitation and Cosmology. John Wiley. pp. 740, 815. ISBN 0-471-92567-5. 
  27. ^ Lemaître, Georges (1933). "The expanding universe". Ann. Soc. Sci. Bruxelles 47A: 49. , English in Gen. Rel. Grav. 29:641-680, 1997.
  28. ^ R. C. Tolman (1934). Relativity, Thermodynamics, and Cosmology. Oxford: Clarendon Press. ISBN 0486653838. LCCN 340-32023.  Reissued (1987) New York: Dover ISBN 0-486-65383-8.
  29. ^ Misner, Charles W.; Leach, P G L (1969). "Mixmaster universe". Phys. Rev. Lett. 22 (15): 1071–74. Bibcode 2008JPhA...41o5201A. doi:10.1088/1751-8113/41/15/155201. 
  30. ^ Dicke, Robert H. (1970). Gravitation and the Universe. Philadelphia: American Philosopical Society. 
  31. ^ Dicke, Robert H.; P. J. E. Peebles (1979). "The big bang cosmology – enigmas and nostrums". In ed. S. W. Hawking and W. Israel. General Relativity: an Einstein Centenary Survey. Cambridge University Press. 
  32. ^ What is the Universe Made Of?
  33. ^ de Sitter, Willem (1917). "Einstein's theory of gravitation and its astronomical consequences. Third paper". Monthly Notices of the Royal Astronomical Society 78: 3–28. Bibcode 1917MNRAS..78....3D. 
  34. ^ Starobinsky, A. A. - Spectrum Of Relict Gravitational Radiation And The Early State Of The Universe - JETP Lett. 30, 682 (1979) {Pisma Zh. Eksp. Teor. Fiz. 30, 719 (1979)}.
  35. ^ SLAC seminar, "10-35 seconds after the Big Bang", 23rd January, 1980. see Guth (1997), pg 186
  36. ^ a b Guth, Alan H. (1981). "Inflationary universe: A possible solution to the horizon and flatness problems" (PDF). Physical Review D 23 (2): 347–356. Bibcode 1981PhRvD..23..347G. doi:10.1103/PhysRevD.23.347. http://www.astro.rug.nl/~weygaert/tim1publication/cosmo2007/literature/inflationary.universe.guth.physrevd-1981.pdf. 
  37. ^ Starobinsky, Alexei A. (1980). "A new type of isotropic cosmological models without singularity". Phys. Lett. B91: 99–102. Bibcode 1980PhLB...91...99S. doi:10.1016/0370-2693(80)90670-X. 
  38. ^ Kazanas, D. (1980). "Dynamics of the universe and spontaneous symmetry breaking". Astrophys. J. 241: L59–63. Bibcode 1980ApJ...241L..59K. doi:10.1086/183361. 
  39. ^ Sato, K. (1981). "Cosmological baryon number domain structure and the first order phase transition of a vacuum". Phys. Lett. B33: 66–70. 
  40. ^ Einhorn, Martin B (1981). "Monopole Production In The Very Early Universe In A First Order Phase Transition". Nucl. Phys. B180 (3): 385–404. Bibcode 1981NuPhB.180..385E. doi:10.1016/0550-3213(81)90057-2. 
  41. ^ Linde, A (1982). "A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems". Physics Letters B 108 (6): 389–393. Bibcode 1982PhLB..108..389L. doi:10.1016/0370-2693(82)91219-9. 
  42. ^ a b Albrecht, Andreas; Steinhardt, Paul (1982). "Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking" (PDF). Physical Review Letters 48 (17): 1220–1223. Bibcode 1982PhRvL..48.1220A. doi:10.1103/PhysRevLett.48.1220. http://astrophysics.fic.uni.lodz.pl/100yrs/pdf/07/060.pdf. 
  43. ^ See Linde (1990) and Mukhanov (2005).
  44. ^ Mukhanov, Viatcheslav F. (1981). "Quantum fluctuation and "nonsingular" universe". JETP Lett. 33: 532–5. Bibcode 1981JETPL..33..532M. 
  45. ^ Mukhanov, Viatcheslav F. (1982). "The vacuum energy and large scale structure of the universe". Sov. Phys. JETP 56: 258–65. 
  46. ^ See Guth (1997) for a popular description of the workshop, or The Very Early Universe, ISBN 0521316774 eds Hawking, Gibbon & Siklos for a more detailed report
  47. ^ Hawking, S.W. (1982). "The development of irregularities in a single bubble inflationary universe". Phys.Lett. B115: 295. 
  48. ^ Starobinsky, Alexei A. (1982). "Dynamics of phase transition in the new inflationary universe scenario and generation of perturbations". Phys. Lett. B117: 175–8. 
  49. ^ Guth, A.H. (1982). "Fluctuations in the new inflationary universe". Phys. Rev. Lett. 49 (15): 1110–3. Bibcode 1982PhRvL..49.1110G. doi:10.1103/PhysRevLett.49.1110. 
  50. ^ Bardeen, James M. (1983). "Spontaneous creation Of almost scale-free density perturbations in an inflationary universe". Phys. Rev. D28: 679. 
  51. ^ a b c d See, e.g. Spergel, D.N. (2006). Three-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Implications for cosmology. http://lambda.gsfc.nasa.gov/product/map/current/map_bibliography.cfm. 
  52. ^ Perturbations can be represented by Fourier modes of a wavelength. Each Fourier mode is normally distributed (usually called Gaussian) with mean zero. Different Fourier components are uncorrelated. The variance of a mode depends only on its wavelength in such a way that within any given volume each wavelength contributes an equal amount of power to the spectrum of perturbations. Since the Fourier transform is in three dimensions, this means that the variance of a mode goes as k−3 to compensate for the fact that within any volume, the number of modes with a given wavenumber k goes as k3.
  53. ^ Tegmark, M. (August 2006). Cosmological constraints from the SDSS luminous red galaxies. arXiv:astro-ph/0608632. Bibcode 2006PhRvD..74l3507T. doi:10.1103/PhysRevD.74.123507. 
  54. ^ a b Steinhardt, Paul J. (2004). "Cosmological perturbations: Myths and facts". Mod. Phys. Lett. A19: 967–82. http://www.worldscinet.com/mpla/19/1913n16/S0217732304014252.html. 
  55. ^ a b c Boyle, Latham A.; Steinhardt, PJ; Turok, N (2006). "Inflationary predictions for scalar and tensor fluctuations reconsidered". Phys. Rev. Lett. 96 (11): 111301. arXiv:astro-ph/0507455. Bibcode 2006PhRvL..96k1301B. doi:10.1103/PhysRevLett.96.111301. PMID 16605810. 
  56. ^ a b Tegmark, Max (2005). "What does inflation really predict?". JCAP 0504 (04): 001. arXiv:astro-ph/0410281. Bibcode 2005JCAP...04..001T. doi:10.1088/1475-7516/2005/04/001. 
  57. ^ This is known as a "red" spectrum, in analogy to redshift, because the spectrum has more power at longer wavelengths.
  58. ^ Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. January 2010. arXiv:1001.4538. Bibcode 2011ApJS..192...18K. doi:10.1088/0067-0049/192/2/18. 
  59. ^ Spergel, D. N.; Verde, L.; Peiris, H. V.; Komatsu, E.; Nolta, M. R.; Bennett, C. L.; Halpern, M.; Hinshaw, G. et al. (2003). "First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: determination of cosmological parameters". Astrophys. J. Suppl. 148 (1): 175. arXiv:astro-ph/0302209. Bibcode 2003ApJS..148..175S. doi:10.1086/377226. http://www.arxiv.org/astro-ph/0302209. 
  60. ^ See cosmic microwave background#Low multipoles for details and references.
  61. ^ Rosset, C.; (PLANCK-HFI collaboration) (2005). "Systematic effects in CMB polarization measurements". Exploring the universe: Contents and structures of the universe (XXXIXth Rencontres de Moriond). 
  62. ^ Loeb, A.; Zaldarriaga, M (2004). "Measuring the small-scale power spectrum of cosmic density fluctuations through 21 cm tomography prior to the epoch of structure formation". Phys. Rev. Lett. 92 (21): 211301. arXiv:astro-ph/0312134. Bibcode 2004PhRvL..92u1301L. doi:10.1103/PhysRevLett.92.211301. PMID 15245272. 
  63. ^ Guth, Alan (1997). The Inflationary Universe. Addison-Wesley. ISBN 0201149427. 
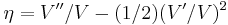  64. ^ Technically, these conditions are that the logarithmic derivative of the potential, \epsilon=(1/2)(V'/V)^2 and second derivative \eta=V''/V-(1/2)(V'/V)^2 are small, where V is the potential and the equations are written in reduced Planck units. See, e.g. Liddle and Lyth (2000).
  65. ^ Linde, Andrei D.; Postma, M (1983). "Chaotic inflation". Phys. Lett. B129 (03): 171–81. Bibcode 2008JCAP...03..015D. doi:10.1088/1475-7516/2008/03/015. 
  66. ^ Technically, this is because the inflaton potential is expressed as a Taylor series in φ/mPl, where φ is the inflaton and mPl is the Planck mass. While for a single term, such as the mass term mφ4(φ/mPl)2, the slow roll conditions can be satisfied for φ much greater than mPl, this is precisely the situation in effective field theory in which higher order terms would be expected to contribute and destroy the conditions for inflation. The absence of these higher order corrections can be seen as another sort of fine tuning. See e.g. Alabidi, Laila; Lyth, David H (2006). "Inflation models and observation". JCAP 0605 (05): 016. arXiv:astro-ph/0510441. Bibcode 2006JCAP...05..016A. doi:10.1088/1475-7516/2006/05/016. 
  67. ^ See, e.g. Lyth, David H. (1997). "What would we learn by detecting a gravitational wave signal in the cosmic microwave background anisotropy?". Phys. Rev. Lett. 78 (10): 1861–3. arXiv:hep-ph/9606387. Bibcode 1997PhRvL..78.1861L. doi:10.1103/PhysRevLett.78.1861. http://www.slac.stanford.edu/spires/find/hep/www?rawcmd=FIND+EPRINT+HEP-PH/9606387. 
  68. ^ Brandenberger, Robert H. (November 2004). "Challenges for inflationary cosmology". 10th International Symposium on Particles, Strings and Cosmology. arXiv:astro-ph/0411671. 
  69. ^ a b Vilenkin, Alexander (1983). "The birth of inflationary universes". Phys. Rev. D27 (12): 2848. Bibcode 1983PhRvD..27.2848V. doi:10.1103/PhysRevD.27.2848. 
  70. ^ A. Linde (1986). "Eternal chaotic inflation". Mod. Phys. Lett. A1: 81. Bibcode 1986MPLA....1...81L. doi:10.1142/S0217732386000129.  A. Linde (1986). "Eternally existing self-reproducing chaotic inflationary universe". Phys. Lett. B175: 395–400. Bibcode 1986PhLB..175..395L. doi:10.1016/0370-2693(86)90611-8. http://www.stanford.edu/~alinde/Eternal86.pdf. 
  71. ^ A. Borde, A. Guth and A. Vilenkin (2003). "Inflationary space-times are incomplete in past directions". Phys. Rev. Lett. 90 (15): 151301. arXiv:gr-qc/0110012. Bibcode 2003PhRvL..90o1301B. doi:10.1103/PhysRevLett.90.151301. PMID 12732026. 
  72. ^ A. Borde (1994). "Open and closed universes, initial singularities and inflation". Phys. Rev. D50: 3692–702. 
  73. ^ A. Borde and A. Vilenkin (1994). "Eternal inflation and the initial singularity". Phys. Rev. Lett. 72 (21): 3305–9. arXiv:gr-qc/9312022. Bibcode 1994PhRvL..72.3305B. doi:10.1103/PhysRevLett.72.3305. 
  74. ^ Linde (2005, §V).
  75. ^ Carroll, Sean M.; Chen, Jennifer (2005). "Does inflation provide natural initial conditions for the universe?". Gen. Rel. Grav. 37 (10): 1671–4. arXiv:gr-qc/0505037. Bibcode 2005GReGr..37.1671C. doi:10.1007/s10714-005-0148-2. 
  76. ^ Carroll, Sean M.. "Spontaneous inflation and the origin of the arrow of time". arXiv:hep-th/0410270. Bibcode 2004hep.th...10270C. 
  77. ^ Anthony Aguirre, Steven Gratton, Inflation without a beginning: A null boundary proposal, Phys.Rev. D67 (2003) 083515, [1]
  78. ^ Anthony Aguirre, Steven Gratton, Steady-State Eternal Inflation, Phys.Rev. D65 (2002) 083507, [2]
  79. ^ J. Hartle and S. W. Hawking, "Wave function of the universe", Phys. Rev. D28, 2960 (1983). See also Hawking (1998).
  80. ^ Hawking (1998), p. 129.
  81. ^ Wikiquote
  82. ^ D.N. Page, "Inflation does not explain time asymmetry", Nature, 304, 39 (1983) see also Roger Penrose's book The Road to Reality: A Complete Guide to the Laws of the Universe.
  83. ^ Hawking, S. W. (1988). "How probable is inflation?". Nucl. Phys. B298 (4): 789. Bibcode 1988NuPhB.298..789H. doi:10.1016/0550-3213(88)90008-9. 
  84. ^ Albrecht, Andreas (2004). "Can the universe afford inflation?". Physical Review D70: 063528. arXiv:hep-th/0405270. Bibcode 2004PhRvD..70f3528A. doi:10.1103/PhysRevD.70.063528. 
  85. ^ Martin, Jerome; Brandenberger, Robert (2001). "The trans-Planckian problem of inflationary cosmology". Phys. Rev. D63 (12): 123501. arXiv:hep-th/0005209. Bibcode 2001PhRvD..63l3501M. doi:10.1103/PhysRevD.63.123501. 
  86. ^ Martin, Jerome; Ringeval, Christophe (2004). "Superimposed Oscillations in the WMAP Data?". Phys. Rev. D69 (8): 083515. arXiv:astro-ph/0310382. Bibcode 2004PhRvD..69h3515M. doi:10.1103/PhysRevD.69.083515. 
  87. ^ Robert H. Brandenberger, "A Status Review of Inflationary Cosmology", proceedings Journal-ref: BROWN-HET-1256 (2001), (available from arXiv:hep-ph/0101119v1 11 January 2001)
  88. ^ Andrei Linde, "Prospects of Inflation", Physica Scripta Online (2004) (available from arXiv:hep-th/0402051 )
  89. ^ Blanco-Pillado et al. , "Racetrack inflation", (2004) (available from arXiv:hep-th/0406230 )
  90. ^ Kachru, Shamit (2003). "Towards inflation in string theory". JCAP 0310: 013. arXiv:hep-th/0308055. Bibcode 2003JCAP...10..013K. doi:10.1088/1475-7516/2003/10/013. 
  91. ^ G. R. Dvali, S. H. Henry Tye, Brane inflation, Phys.Lett. B450, 72-82 (1999), arXiv:hep-ph/9812483.
  92. ^ Earman, John and Jesús Mosterín (1999). “A Critical Look at Inflationary Cosmology”. Philosophy of Science, 66 (March), pp. 1-49.
  93. ^ Penrose, Roger (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. London: Vintage Books, p. 755. See also Penrose, Roger (1989). “Difficulties with Inflationary Cosmology”. Annals of the New York Academy of Sciences, 271, pp. 249-264.
  94. ^ Steinhardt, Paul J. (2011). “The inflation debate: Is the theory at the heart of modern cosmology deeply flawed?” (Scientific American, April; pp. 18-25). See also: Steinhardt, Paul J. and Neil Turok (2007). Endless Universe: Beyond the Big Bang. Doubleday, 2007.
  95. ^ Brandenberger, R (1989). "Superstrings in the early universe". Nuclear Physics B 316 (2): 391–410. Bibcode 1989NuPhB.316..391B. doi:10.1016/0550-3213(89)90037-0. 
  96. ^ Thorsten Battefeld and Scott Watson, String Gas Cosmology, Rev. Mod. Phys 78, 435-454 (2006), arXiv:hep-th/0510022
  97. ^ Robert H. Brandenberger, Ali Nayeri, Subodh P. Patil and Cumrun Vafa, String Gas Cosmology and Structure Formation, Int.J.Mod.Phys.A22:3621-3642,2007., arXiv:hep-th/0608121.

References

External links